딥러닝 구성 요소
1. 핵심 구성 요소:
- 데이터 (Data):
- 모델 학습에 필요한 데이터.
- 예시: MNIST, Fashion MNIST 등.
- 모델 (Model):
- 주어진 데이터를 원하는 결과로 변환하는 역할.
- 다층 퍼셉트론 (MLP), 컨볼루션 신경망 (CNN), 순환 신경망 (RNN) 등 다양한 구조가 있음.
- 손실 함수 (Loss Function):
- 모델의 결과 (예측)와 실제 값 사이의 오차를 수치화.
- 평균 제곱 오차 (MSE), 교차 엔트로피 (Cross-Entropy) 등.
- 최적화 알고리즘 (Optimization Algorithm):
- 손실 함수의 값을 최소화하도록 모델의 파라미터(가중치, 편향)를 조정.
- 경사 하강법 (GD), 확률적 경사 하강법 (SGD), 모멘텀 (Momentum) 등.
2. 딥러닝 성능:
- 딥러닝의 성능은 모델(구조), 데이터, 학습 방법(손실 함수, 최적화 알고리즘, 기타 알고리즘)에 의해 결정됨.
3. 성능 향상을 위한 기타 알고리즘:
- 과적합(Overfitting) 방지: Dropout, Regularization(L1, L2 규제).
- 학습 가속화 및 안정화: Batch Normalization, Layer Normalization 등.
퍼셉트론 (Perceptrons)
퍼셉트론의 작동 방식
- 입력 신호: 퍼셉트론은 여러 개의 입력 신호(x1, x2, ..., xn)를 받습니다. 각 입력 신호는 0 또는 1의 값을 가집니다.
- 가중치: 각 입력 신호에는 가중치(w1, w2, ..., wn)가 할당됩니다. 가중치는 각 신호가 출력에 미치는 영향력을 나타냅니다.
- 가중치 합: 각 입력 신호와 그에 해당하는 가중치를 곱한 후 모두 더합니다. 이를 가중치 합이라고 합니다.
- 활성화 함수: 가중치 합은 활성화 함수에 입력됩니다. 활성화 함수는 임계값(θ)을 기준으로 출력 값을 결정합니다.
- 가중치 합이 임계값보다 크면 1을 출력합니다.
- 가중치 합이 임계값보다 작으면 0을 출력합니다.

가중치란?
가중치는 퍼셉트론에서 각 입력 신호가 출력에 미치는 영향력을 나타내는 값입니다. 각 입력 신호에는 가중치가 곱해지며, 가중치가 클수록 해당 신호는 출력에 더 큰 영향을 미칩니다. 가중치는 퍼셉트론 학습 과정에서 조정되며, 이를 통해 퍼셉트론은 입력 신호와 출력 신호 간의 관계를 학습합니다.
편향이란?
편향은 퍼셉트론에서 활성화 함수가 발동하는 정도를 조절하는 값입니다. 편향은 입력 신호와 독립적으로 출력에 더해지며, 편향이 클수록 퍼셉트론은 더 쉽게 활성화됩니다. 편향 또한 퍼셉트론 학습 과정에서 조정되며, 이를 통해 퍼셉트론은 입력 신호가 없는 경우에도 출력을 조절할 수 있습니다.
가중치와 편향의 역할
- 가중치: 각 입력 신호의 중요도를 조절합니다.
- 편향: 퍼셉트론의 활성화 정도를 조절합니다.
퍼셉트론과 선형 분리
퍼셉트론은 입력 신호에 가중치를 곱하고 합한 값을 활성화 함수에 통과시켜 출력을 결정합니다. 이 과정은 2차원 평면에서 직선의 방정식을 구하는 것과 유사합니다. 따라서 퍼셉트론은 선형 분리 가능한 데이터를 분류하는 데 사용할 수 있습니다.
퍼셉트론의 한계
퍼셉트론은 선형 분리 가능한 데이터만 분류할 수 있다는 한계가 있습니다. 예를 들어, XOR 문제와 같이 선형적으로 분리할 수 없는 데이터는 퍼셉트론으로 분류할 수 없습니다.
다층 퍼셉트론 (Multi-Layer Perceptron, MLP)
퍼셉트론을 여러 층으로 쌓아 만든 인공신경망입니다. 퍼셉트론은 선형으로 분리 가능한 데이터만 분류할 수 있다는 한계가 있지만, 다층 퍼셉트론은 여러 개의 은닉층을 추가하여 비선형적인 데이터도 분류할 수 있습니다.
Fully-Connected Layers(FCs)의 동의어로 사용된다.
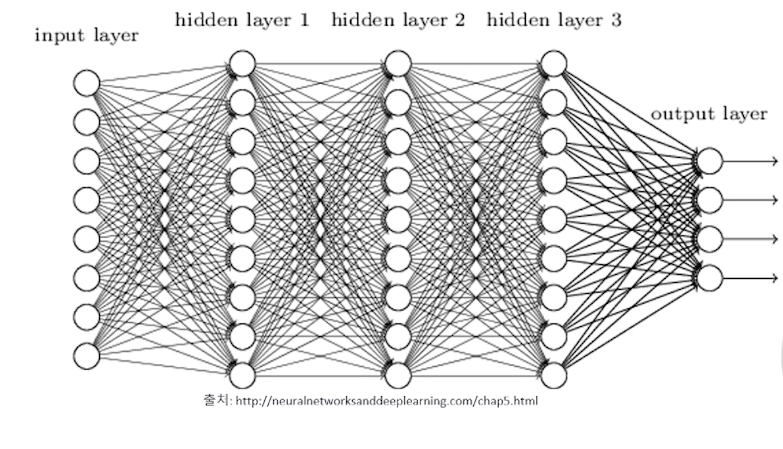
다층 퍼셉트론의 구조
다층 퍼셉트론은 일반적으로 다음과 같은 3개의 층으로 구성됩니다.
- 입력층(Input Layer): 데이터를 입력받는 층입니다.
- 은닉층(Hidden Layer): 입력층과 출력층 사이에 있는 층으로, 여러 개의 퍼셉트론으로 구성됩니다. 은닉층은 입력 데이터의 특징을 추출하는 역할을 합니다.
- 출력층(Output Layer): 최종 결과를 출력하는 층입니다.
활성화 함수 사용 이유
1. 비선형성 도입
- 선형 모델의 한계: 만약 활성화 함수가 없다면, 신경망은 단순히 선형적인 연산만 수행하게 됩니다. 즉, 입력과 출력이 선형적인 관계를 가지게 되어 복잡한 패턴을 학습할 수 없습니다.
- 비선형성: 활성화 함수는 입력 신호를 비선형적으로 변환하여 신경망에 비선형성을 추가합니다. 이를 통해 신경망은 복잡한 데이터 간의 관계를 학습하고, 비선형적인 문제를 해결할 수 있습니다.
2. 복잡한 패턴 학습
- 단순한 분류: 선형 모델은 단순한 분류 문제만 해결할 수 있습니다.
- 패턴 학습: 활성화 함수는 신경망이 복잡한 패턴을 학습할 수 있도록 도와줍니다. 예를 들어, 이미지 인식에서 활성화 함수는 이미지의 특징을 추출하고, 이를 바탕으로 이미지를 분류하는 데 중요한 역할을 합니다.
3. 출력 값 조절
- 출력 범위 제한: 일부 활성화 함수는 출력 값의 범위를 제한합니다. 예를 들어, 시그모이드 함수는 출력 값을 0과 1 사이로 제한하여 확률 값으로 해석할 수 있도록 합니다.
- 의사 결정: 활성화 함수는 특정 임계값을 기준으로 출력을 결정하는 데 사용될 수 있습니다. 예를 들어, 계단 함수는 입력 값이 임계값보다 크면 1을 출력하고, 작으면 0을 출력하여 이진 분류 문제에 사용될 수 있습니다.
4. 효율적인 학습
- 미분 가능: 일부 활성화 함수는 미분이 가능합니다. 이는 역전파 알고리즘을 통해 신경망을 효율적으로 학습시키는 데 중요한 역할을 합니다.
- 최적화: 미분 가능한 활성화 함수는 경사 하강법과 같은 최적화 알고리즘을 사용하여 가중치를 효율적으로 업데이트하고, 모델의 성능을 향상시키는 데 도움을 줍니다.
활성화 함수 종류
1. 계단 함수 (Step Function)
- 특징: 입력 값이 특정 임계값을 넘으면 1을 출력하고, 그렇지 않으면 0을 출력하는 가장 단순한 형태의 활성화 함수입니다.
- 장점: 직관적이고 이해하기 쉽습니다.
- 단점: 미분 불가능하여 역전파 알고리즘을 사용할 수 없습니다. 또한, 출력이 0 또는 1로 제한되어 다양한 표현력을 가지기 어렵습니다.
2. 시그모이드 함수 (Sigmoid Function)
- 특징: 입력 값을 0과 1 사이의 값으로 변환하는 S자 형태의 함수입니다.
- 장점: 출력이 확률 값으로 해석될 수 있으며, 미분이 가능하여 역전파 알고리즘을 사용할 수 있습니다.
- 단점: 입력 값이 극단적으로 커지거나 작아지면 기울기가 0에 가까워져 학습이 느려지거나 멈추는 기울기 소실 문제가 발생할 수 있습니다.
3. 하이퍼볼릭 탄젠트 함수 (Hyperbolic Tangent Function)
- 특징: 입력 값을 -1과 1 사이의 값으로 변환하는 함수입니다.
- 장점: 시그모이드 함수와 유사하지만, 출력 값의 범위가 -1에서 1 사이이므로 기울기 소실 문제가 덜 발생합니다.
- 단점: 여전히 기울기 소실 문제가 발생할 수 있습니다.
4. ReLU 함수 (Rectified Linear Unit Function)
- 특징: 입력 값이 0보다 작으면 0을 출력하고, 0보다 크면 입력 값을 그대로 출력하는 함수입니다.
- 장점: 기울기 소실 문제를 완화하고, 학습 속도를 향상시킵니다.
- 단점: 입력 값이 0보다 작은 경우 기울기가 0이 되어 뉴런이 죽는 현상이 발생할 수 있습니다.
5. Leaky ReLU 함수 (Leaky Rectified Linear Unit Function)
- 특징: ReLU 함수의 단점을 보완하기 위해, 입력 값이 0보다 작은 경우에도 아주 작은 기울기를 가지도록 변형한 함수입니다.
- 장점: ReLU 함수의 장점을 유지하면서 뉴런이 죽는 현상을 완화합니다.
6. 소프트맥스 함수 (Softmax Function)
- 특징: 여러 개의 출력 값을 정규화하여 각 출력 값의 합이 1이 되도록 만드는 함수입니다. 주로 다중 분류 문제에서 출력층의 활성화 함수로 사용됩니다.
- 장점: 다중 분류 문제에서 각 클래스에 대한 확률 값을 얻을 수 있습니다.
미분 (differentiation)
함수의 순간적인 변화율을 분석하는 데 사용됩니다. 어떤 함수의 특정 지점에서의 기울기 또는 변화 속도를 구하는 것을 의미합니다.
'공부' 카테고리의 다른 글
| 프로젝트를 위한 협업: Github (0) | 2024.12.16 |
|---|---|
| 버전관리 - Git, Github 이론 (0) | 2024.12.12 |
| 복습 목차 (0) | 2024.12.12 |
| HTTP의 특성 (0) | 2024.12.12 |
| 웹 서버와 웹 어플리케이션 서버 (0) | 2024.12.12 |