노름(Norm)
노름(Norm) 이란 벡터의 크기 또는 길이를 측정하는 방법입니다. 벡터가 원점에서 얼마나 떨어져 있는지 나타내는 값이라고 생각할 수 있습니다.
노름의 종류
노름에는 여러 가지 종류가 있으며, 가장 일반적으로 사용되는 노름은 다음과 같습니다.
- L1 노름: 각 성분의 절댓값의 합입니다. 맨해튼 거리라고도 합니다.
- L2 노름: 각 성분의 제곱의 합의 제곱근입니다. 유클리드 거리라고도 합니다.
- L∞ 노름: 각 성분의 절댓값 중 가장 큰 값입니다. 최대 노름이라고도 합니다.

||x||p: 벡터 x의 Lp 노름
n: 벡터 x의 차원 (성분의 개수)
xi: 벡터 x의 i번째 성분
p: 노름의 차수 (1, 2, ∞ 등)
L1 노름 수식


L2 노름


L∞ 노름


노름에 따른 기하학적 의미

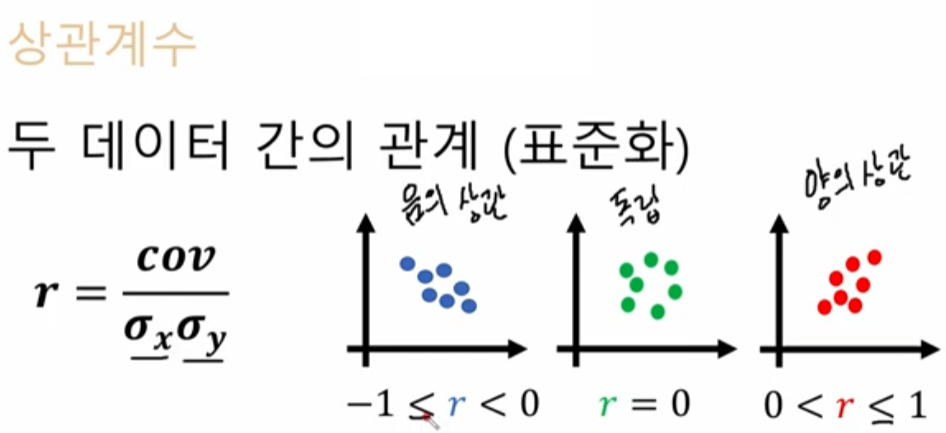
유사도
유사도(Similarity) 란 두 벡터가 얼마나 유사한지에 대한 측정값을 의미합니다.
군집화(Clustering) 알고리즘에서 데이터들이 얼마나 유사한지를 판단하는 중요한 기준으로 사용됩니다.
군집화는 비지도 학습의 한 형태로서, 유사한 데이터들을 그룹으로 묶는 기법입니다. 예를 들어, 고객들의 구매 패턴을 분석하여 유사한 고객들을 그룹으로 묶거나, 문서들을 주제별로 분류하는 데 사용될 수 있습니다.
맨해튼 유사도
두 점 사이의 거리를 맨해튼 거리(Manhattan distance)를 사용하여 계산하고, 이를 통해 유사도를 측정하는 방법
수식

두 벡터 x와 y 사이의 맨해튼 거리
distance(x, y) = |x1 - y1| + |x2 - y2| + ... + |xn - yn|
맨해튼 유사도는 맨해튼 거리에 반비례합니다. 즉, 맨해튼 거리가 작을수록 유사도가 높습니다.
맨해튼 유사도를 0과 1 사이의 값으로 정규화
similarity(x, y) = 1 / (1 + distance(x, y))
코드
# 맨해튼 유사도의 코드 표현 실습
import torch
b = torch.tensor([1, 0, 2], dtype=torch.float32)
c = torch.tensor([0, 1, 2], dtype=torch.float32)
# 맨해튼 거리 계산
manhattan_distance = torch.norm(b - c, p = 1)
# 유사도 계산 (예시: 거리의 역수)
manhattan_similarity = 1 / (1 + manhattan_distance)
print(f'Manhattan Distance: {manhattan_distance}')
print(f'Manhattan Similarity: {manhattan_similarity}')Manhattan Distance: 2.0
Manhattan Similarity: 0.3333333432674408
유클리드 유사도
두 점 사이의 거리를 유클리드 거리(Euclidean distance)를 사용하여 계산하고, 이를 통해 유사도를 측정하는 방법입니다. 유클리드 거리는 두 점 사이의 직선 거리를 의미하며, 피타고라스 정리를 사용하여 계산합니다.
수식

두 벡터 p와 q 사이의 유클리드 거리
d(p, q) = sqrt((p1 - q1)^2 + (p2 - q2)^2 + ... + (pn - qn)^2)
0과 1 사이의 값으로 정규화
similarity(p, q) = 1 / (1 + d(p, q))
코드
# 유클리드 유사도의 코드 표현 실습
import torch
b = torch.tensor([1, 0, 2], dtype=torch.float32)
c = torch.tensor([0, 1, 2], dtype=torch.float32)
# 유클리드 거리 계산
euclidean_distance = torch.norm(b - c, p = 2)
# 유사도 계산 (예시: 거리의 역수)
euclidean_similarity = 1 / (1 + euclidean_distance)
print(f'Euclidean Distance: {euclidean_distance.item()}')
print(f'Euclidean Similarity: {euclidean_similarity.item()}')Euclidean Distance: 1.4142135381698608
Euclidean Similarity: 0.41421353816986084
코사인 유사도 (★ ★ ★ ★ ★)
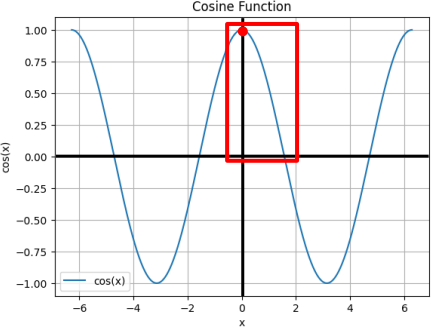
코사인 유사도는 두 벡터 사이의 각도의 코사인 값을 이용하여 유사도를 측정하는 방법입니다. 두 벡터의 방향이 완전히 같으면 1, 완전히 반대 방향이면 -1, 직교하면 0의 값을 갖습니다. 즉, 두 벡터가 이루는 각이 작을수록 (1에 가까울수록) 유사도가 높다고 판단합니다.
언어모델에서는 양의 수를 사용 (0 ~ 1)
수식
similarity(p, q) = (p · q) / (||p|| ||q||)
p · q는 두 벡터의 내적(dot product)을 의미
||p||는 벡터 p의 크기(magnitude)를 의미
||q||는 벡터 q의 크기(magnitude)를 의미
벡터의 내적과 크기는 다음과 같이 계산합니다.
p · q = p1 * q1 + p2 * q2 + ... + pn * qn
||p|| = sqrt(p1^2 + p2^2 + ... + pn^2)
||q|| = sqrt(q1^2 + q2^2 + ... + qn^2)
벡터의 내적 구하는 2가지 방법
방법1
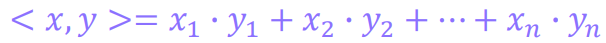
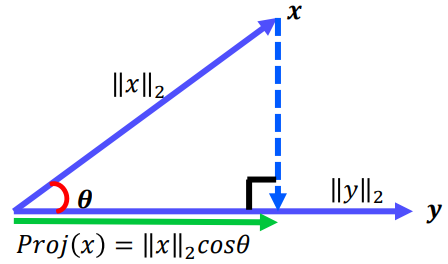
방법2
코드
# 코사인 유사도의 코드 표현 실습
b = torch.tensor([1, 0, 2], dtype=torch.float32)
c = torch.tensor([0, 1, 2], dtype=torch.float32)
# 코사인 유사도 계산
dot_product = torch.dot(b, c)
norm_b = torch.norm(b, p = 2)
norm_c = torch.norm(c, p = 2)
cosine_similarity = dot_product / (norm_b * norm_c)
print(f'Cosine Similarity: {cosine_similarity}')Cosine Similarity: 0.800000011920929
감성분석
텍스트를 대상으로 해당 텍스트가 긍정 or 중립 or 부정 인지를 판단하는 분석
여기에서는 코사인 유사도가 정확하게 나옴
행렬의 곱셈 연산
두 행렬을 결합하여 새로운 행렬을 생성하는 연산
신경망 구현에 핵심이 되는 연산
행렬을 더하면 이미지 두개를 합성하는 것
이미지에서 부분을 제거하고 싶으면 행렬의 뺄샘 사용
달콤, 세피아의 경우 이미지에 스칼라를 곱하면 됨
행렬 A와 B의 곱 AB를 구하려면, A의 열의 개수와 B의 행의 개수가 같아야 합니다.
만약 A가 m x n 행렬이고 B가 n x p 행렬이라면, 곱 AB는 m x p 행렬이 됩니다.

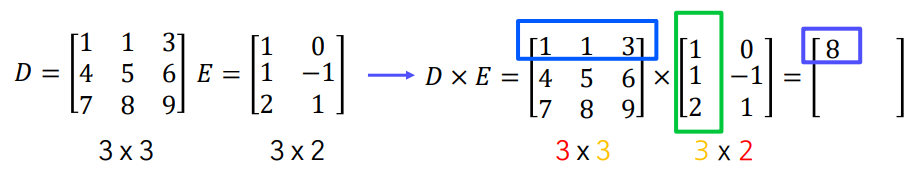
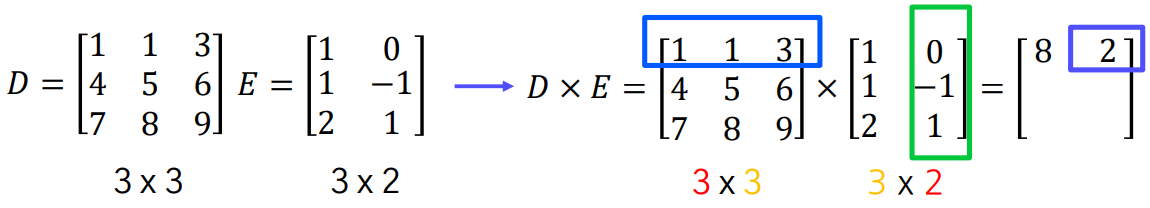
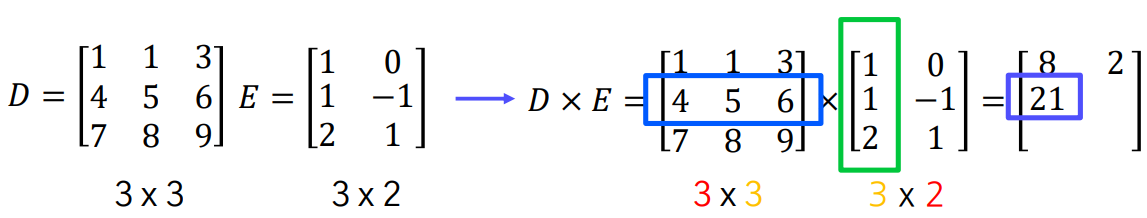
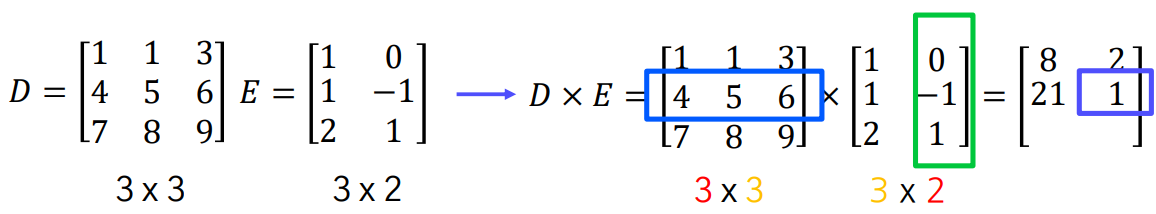
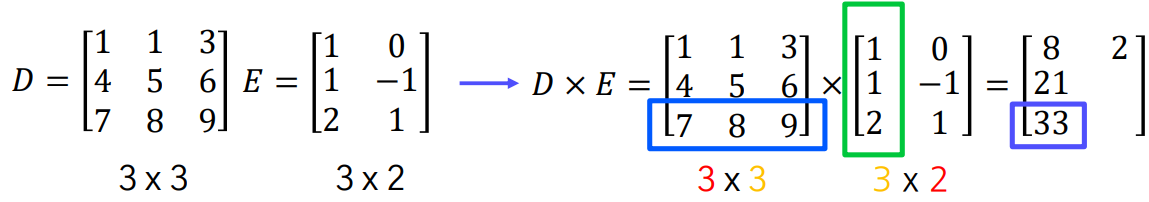
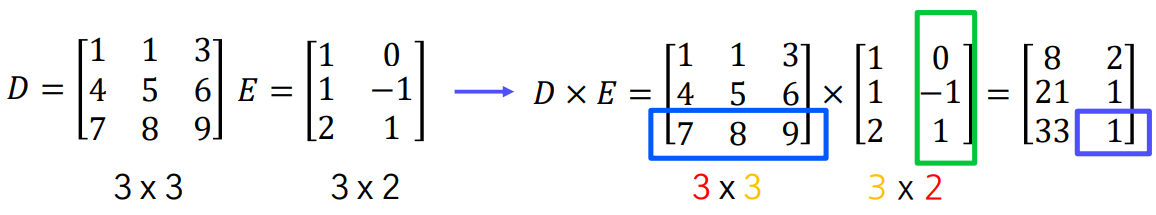

흑백이미지의 대칭 이동(반사)
좌우대칭
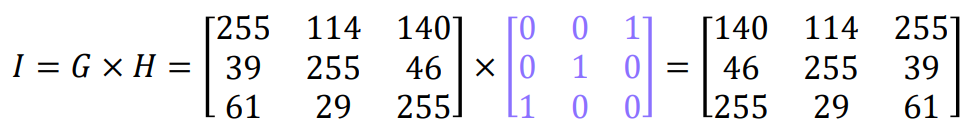
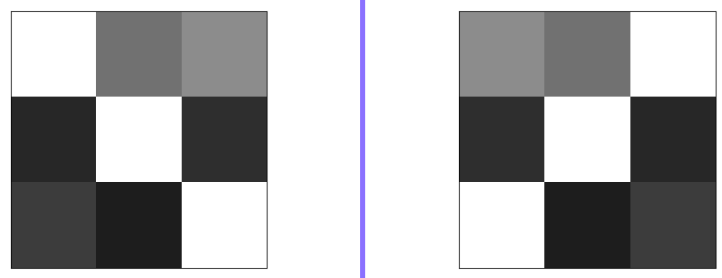
코드
import torch
import matplotlib.pyplot as plt
G = torch.tensor([[255, 114, 140],
[39, 255, 46],
[61, 29, 255]])
plt.xticks([]), plt.yticks([])
plt.imshow(G, cmap='gray', vmin=0, vmax=255)
plt.show()
H = torch.tensor([[0, 0, 1],
[0, 1, 0],
[1, 0, 0]])
I = G @ H
plt.xticks([]), plt.yticks([])
plt.imshow(I, cmap='gray', vmin=0, vmax=255)
plt.show()
평균 벡터 (Mean Vector)
평균 벡터란 주어진 벡터들의 중심 또는 평균위치 를 나타내는 벡터를 의미함
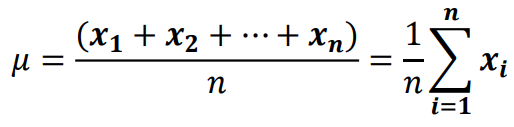
예시)
세 개의 벡터 v1 = (1, 2), v2 = (3, 4), v3 = (5, 6) 이 있다고 가정해 봅시다. 이 벡터들의 평균 벡터는 다음과 같이 계산합니다.
- 각 성분들을 더합니다: (1 + 3 + 5, 2 + 4 + 6) = (9, 12)
- 벡터의 개수로 나눕니다: (9 / 3, 12 / 3) = (3, 4)
따라서 평균 벡터는 (3, 4)입니다.
공분산 (Covariance)
공분산은 두 변수가 함께 어떻게 변하는지를 측정하는 값입니다. 즉, 한 변수의 변화가 다른 변수의 변화에 어떤 영향을 미치는지를 나타냅니다.
좀 더 쉽게 설명하면, 두 변수가 같은 방향으로 움직이는 경향이 있는지, 반대 방향으로 움직이는 경향이 있는지, 아니면 서로 관계없이 움직이는지를 알려줍니다.
공분산의 계산
- 각 변수의 편차를 계산합니다. (편차 = 데이터 값 - 평균)
- 두 변수의 편차를 곱합니다.
- 모든 데이터 포인트에 대해 2번의 결과를 더합니다.
- 데이터 포인트의 개수로 나눕니다.
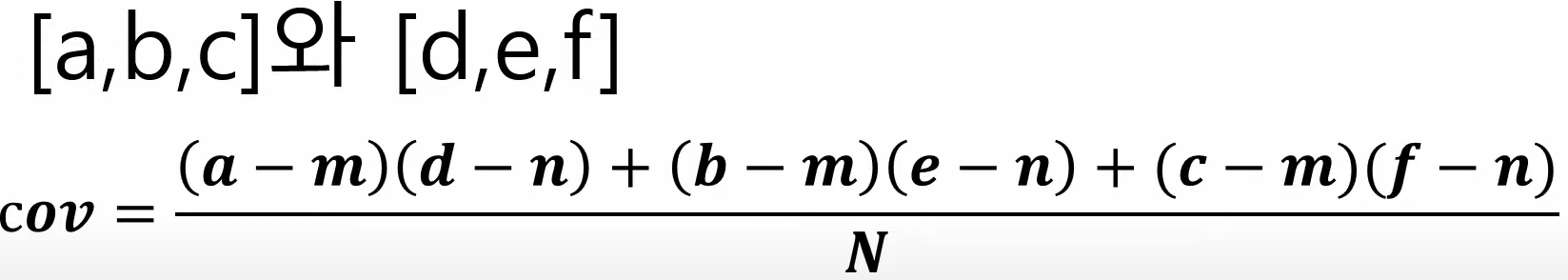
m = a,b,c 의 평균
n = d,e,f 의 평균
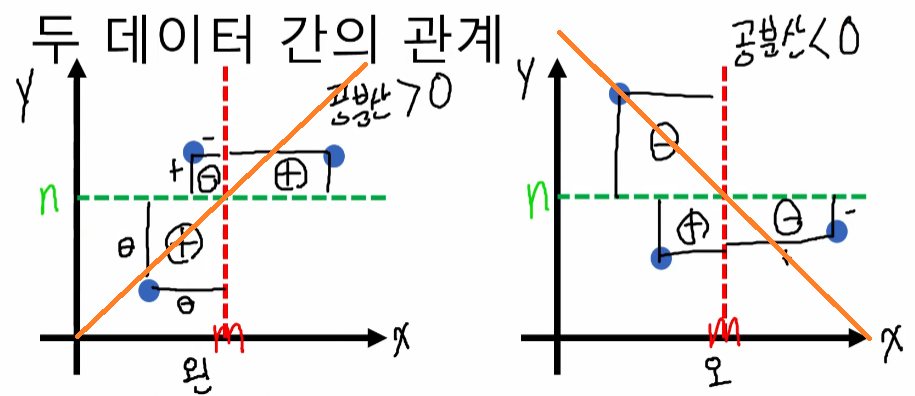
공분산의 값
- 양수: 두 변수가 같은 방향으로 움직이는 경향이 있습니다. 한 변수가 증가하면 다른 변수도 증가하는 경향을 보입니다.
- 음수: 두 변수가 반대 방향으로 움직이는 경향이 있습니다. 한 변수가 증가하면 다른 변수는 감소하는 경향을 보입니다.
- 0에 가까운 값: 두 변수 간에 선형적인 관계가 거의 없습니다. 서로 독립적으로 움직입니다.
문제)
[1,2,3] 와 [1,3,5]의 공분산은?
m = 2
n = 3
=> (-1x-2 + 0x0 + 1x2) / 3
=> (2 + 2) / 3
=> 4/3
공분산 행렬 (Covariance Matrix)
공분산 행렬은 여러 변수들 간의 공분산을 행렬 형태로 나타낸 것입니다.
예를 들어, 키, 몸무게, 나이 세 가지 변수가 있다면 3x3 공분산 행렬은 다음과 같습니다.

- 대각선: 각 변수의 분산 (Var)을 나타냅니다. 즉, 해당 변수가 얼마나 퍼져 있는지 보여줍니다.
- 대각선 외: 두 변수 간의 공분산 (Cov)을 나타냅니다. 즉, 두 변수가 얼마나 관련되어 있는지 보여줍니다.
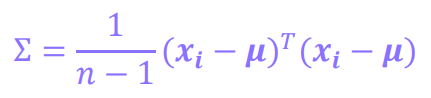
NumPy cov() 함수 사용
import numpy as np
# 데이터 정의
x = np.array([[1, 2, 3],
[2, 2, 4],
[1, 1, 2],
[0, 3, 3]])
# 공분산 행렬 계산
cov_matrix = np.cov(x, rowvar=False)
# 결과 출력
print(cov_matrix)[[ 0.66666667 -0.33333333 0.33333333]
[-0.33333333 0.66666667 0.33333333]
[ 0.33333333 0.33333333 0.66666667]]
확률 변수 Random Variable
어떤 확률적 현상의 결과를 숫자로 나타낸 것
- 이산 확률 변수: 가질 수 있는 값이 유한하거나 셀 수 있을 만큼 무한한 확률 변수입니다. 예를 들어, 주사위를 던져 나오는 눈의 수, 동전을 던져 앞면이 나오는 횟수 등이 이산 확률 변수입니다.
- 연속 확률 변수: 가질 수 있는 값이 연속적인 구간에 속하는 확률 변수입니다. 예를 들어, 사람의 키, 몸무게, 온도 등이 연속 확률 변수입니다.
확률 함수
확률 변수가 특정 값을 가질 확률을 나타내는 함수
1. 확률 질량 함수 (Probability Mass Function, PMF)
- 이산 확률 변수에 대한 확률 함수입니다.
- 확률 변수가 특정 값을 가질 확률을 나타냅니다.
- 예를 들어, 주사위를 던져서 나오는 눈의 수를 확률 변수 X라고 하면, X의 확률 질량 함수는 다음과 같습니다.


2. 확률 밀도 함수 (Probability Density Function, PDF)
- 연속 확률 변수에 대한 확률 함수입니다.
- 확률 변수가 특정 구간에 속할 확률을 나타냅니다.
- 연속 확률 변수는 특정 값을 가질 확률이 0이기 때문에, 확률 밀도 함수는 특정 값에서의 확률을 나타내는 것이 아니라, 특정 구간에서의 확률을 나타냅니다.
- 확률 밀도 함수는 다음과 같은 특징을 갖습니다.
- 항상 0보다 크거나 같습니다.
- 전체 구간에 대한 적분 값은 1입니다.
- 예를 들어, 키를 확률 변수 X라고 하면, X의 확률 밀도 함수는 특정 키 범위에 속할 확률을 나타냅니다.
사건, 확률변수, 확률, 확률함수의 관계
동전을 두 번 던져 앞면이 나오는 경우를 기준으로 사건, 확률변수, 확률, 확률함수 의 관계를 설명해 드리겠습니다.
1. 사건
동전을 두 번 던졌을 때 발생할 수 있는 모든 경우의 수를 사건이라고 합니다.
- HH (앞면, 앞면)
- HT (앞면, 뒷면)
- TH (뒷면, 앞면)
- TT (뒷면, 뒷면)
총 4가지 사건이 존재합니다.
2. 확률 변수
각 사건에 대해 특정 값을 부여하는 변수를 확률 변수라고 합니다. 여기서는 앞면이 나온 횟수를 확률 변수 X로 정의할 수 있습니다.
- HH: X = 2 (앞면이 2번)
- HT, TH: X = 1 (앞면이 1번)
- TT: X = 0 (앞면이 0번)
3. 확률
각 사건이 발생할 가능성을 확률이라고 합니다. 동전이 공정하다면 각 사건이 발생할 확률은 모두 1/4로 동일합니다.
- P(HH) = 1/4
- P(HT) = 1/4
- P(TH) = 1/4
- P(TT) = 1/4
4. 확률 함수
확률 변수가 특정 값을 가질 확률을 나타내는 함수를 확률 함수라고 합니다.
- P(X = 0) = P(TT) = 1/4
- P(X = 1) = P(HT) + P(TH) = 1/2
- P(X = 2) = P(HH) = 1/4
적분의 필요성
다양한 모양의 넓이를 구하기 위해
확률변수의 평균
기대값과 같은 의미로 사용됨
기대값이란 어떤 사건에 대하여 해당 사건이 벌어질 확률을 곱해서 전체 사건에 대하여 합한 값을 의미
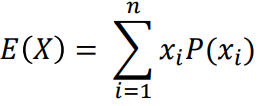
주사위를 던질 때 확률변수의 평균
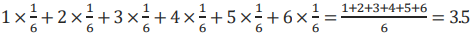
확률변수의 평균의 성질
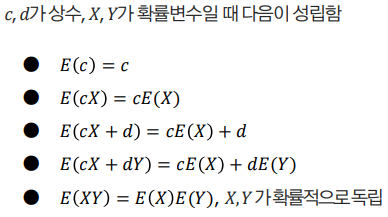
문제)

E(3) = ?
E(3)은 상수 3의 기댓값이므로, E(3) = 3 입니다.
E(3X - 2) = ?
E(3X - 2) = E(3X) - E(2) (기댓값의 성질)
= 3E(X) - 2 (기댓값의 성질)
= 3 * 3 - 2 (E(X) = 3 대입)
= 9 - 2
= 7
E(-2X + 1) = ?
E(-2X + 1) = E(-2X) + E(1) (기댓값의 성질)
= -2E(X) + 1 (기댓값의 성질)
= -2 * 3 + 1 (E(X) = 3 대입)
= -6 + 1
= -5
확률변수의 분산
확률변수들이 기대값으로부터 벗어난 정도
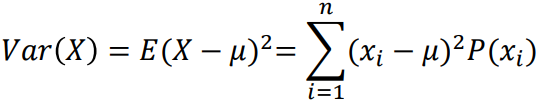
주사위를 던질 때 확률변수의 분산 식
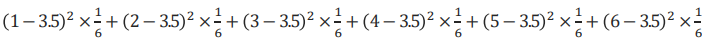
확률변수의 분산의 성질

문제)

V(3) = 0
V(3X) = 45
V(3X - 1) = 45
확률변수의 표준편차
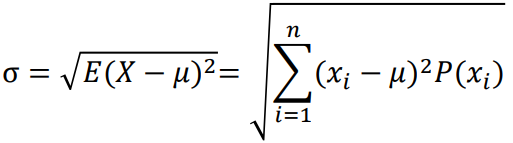
확률 분포
확률 분포는 확률 변수가 가질 수 있는 모든 값과 그 값에 해당하는 확률을 나타내는 함수 또는 표입니다.
(확률분포는 전체, 확률함수는 각각)
동전을 던지는 경우의 확률분포
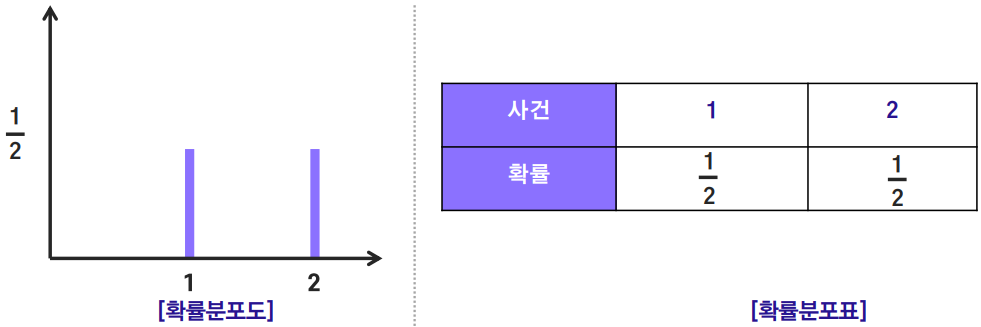
균등 분포
특정 범위 내에서 모든 값이 나타날 확률이 동일한 분포
이산 균등분포
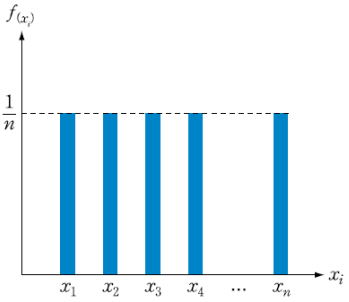
연속 균등분포
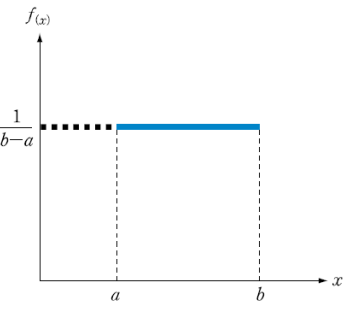
정규 분포
표본분포 중 가장 단순하면서 많이 나타나는 형태의 분포
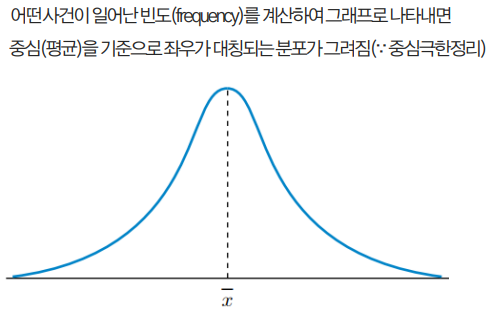
정규분포의 성질
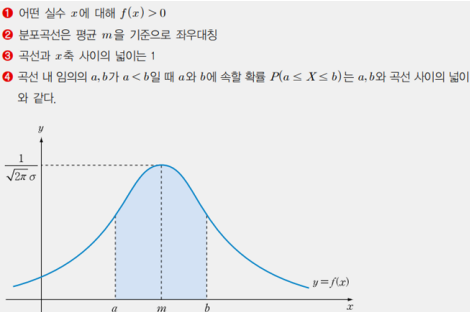
표준정규분포

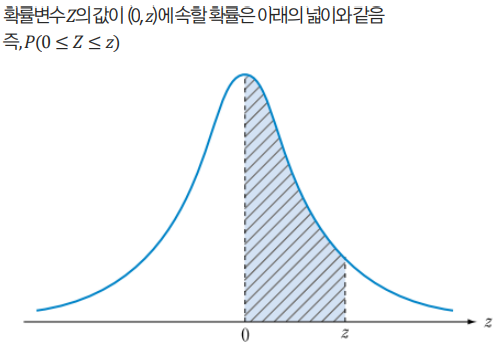
정규분포 실습 코드
import numpy as np
import matplotlib.pyplot as plt
mu, sigma = 0, 0.1
s = np.random.normal(mu, sigma, 1000)
count, bins, ignored = plt.hist(s, 30, density=True)
plt.plot(bins, 1/(sigma*np.sqrt(2*np.pi))*
np.exp(- (bins - mu)**2 / (2*sigma**2)), linewidth=2, color='r')
plt.show()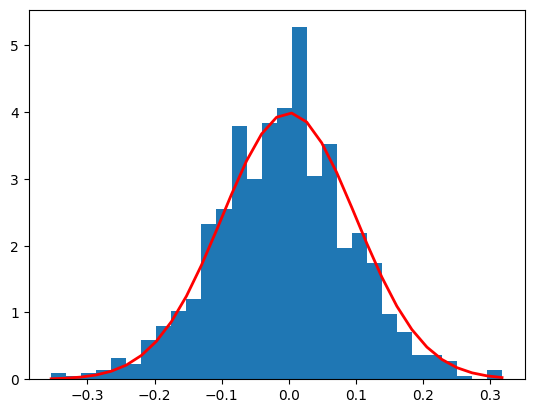
꼭 알고 넘어가야할 개념들 (요약)
사건
확률변수
확률함수
확률변수의 평균(기대값)
확률변수의 분산
정규분포
정규분포 표준화 (0~1)
베르누이 시행
서로 반대되는 사건이 일어나는 시행을 반복적으로 실행하는 것
서로 반대되는 사건이란 반드시 두 가지만 존재하며 동시에 일어나지 않는 배타적인 사건을 의미함
예) 동전 던지기
베르누이 분포 (중요)
베르누이 시행을 확률분포로 나타낸 것
성공확률을 p(x = 1 경우) 라 할때,
실패확률은 1 - p(x = 1 경우)로 가정
베르누이 분포의 평균과 분산
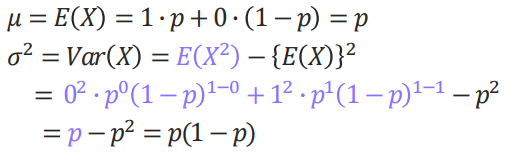
이항분포
연속적인 베르누이 시행을 통해 표현된 확률분포
서로 독립적인 베르누이 시행을 n회 반복하여 성공한 횟수를 X라 할 때,
성공한 X의 확률분포를 이항분포라 함
이항분포의 평균과 분산
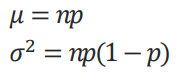
성공확률 p에 대하여 베르누이 시행을 n회 반복한 이항분포를
X~B(n,p)와 같이 표현함
이항분포 확률의 계산
이항분포의 확률은 n번의 시행에서 성공확률(p)이 r번 나타날 확률이므로, n번의 시행에서 r번 관찰되는 것으로 표현 가능함
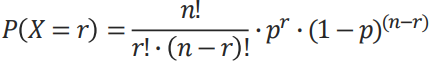
이항분포 문제
S 선수가 패널티킥을 차면 5번중 4번을 성공한다고 한다.
S 선수가 10번을 차서 7번을 성공할 확률을 구하시오.
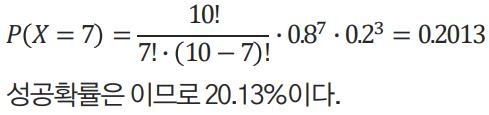
기술통계와 추리통계
통계: 여러 가지 현상에 대하여 수리적으로 정리, 분석, 예측하는 작업
기술통계: 수집된 자료의 특성을 요약 정리하는 것이 목적
- 중심경향도: 평균, 중앙값, 최빈값 등 데이터의 중심적인 경향을 나타내는 값
- 산포도: 범위, 분산, 표준편차 등 데이터가 얼마나 퍼져 있는지를 나타내는 값
추리통계: 분석된 자료를 근거로 모집단의 특성을 추론하는 것이 목적
점추정, 구간추정: 모집단의 특성을 추정하는 방법
추정 관련 용어
추정: 추정이란 어떠한 정도를 가늠하는 방법으로 수치로 나타내거나, 범위로 나타낼 수 있음
점추정: 모수를 어떤 특정 수치로 표현하는 것
학교 시험에서 획득할 평균 점수를 80점, 90점과 같이 특정 수치로 표현
구간추정: 모수를 최소값과 최대값의 범위로 표현하는 것
학교 시험에서 획득할 평균 점수를 80~90점과 같이 범위로 표현
추정량: 표본으로부터 관찰된 값을 토대로 특정 모수를 추정하기 위한 함수 또는 공식을 의미함
예) 모집단의 평균을 추정할 때, 표본 평균(𝑥̄)을 구하는 공식을 추정량이라고 부름
추정치: 추정량을 사용해 실제 표본 데이터에서 계산된 값을 의미함
예) 표본 평균(𝑥̄)을 구하는 공식을 추정량으로 사용할 때, 특정 표본 데이터를 이용해 계산한 평균값이 추정치임
점추정
바람직한 점추정량 조건(중요하지 않음)
점추정은 잘 사용하지 않음
구간추정
점추정의 한계: 점추정은 모수를 하나의 값으로 추정하기 때문에 간편하고 이해하기 쉽지만, 추정값이 실제 모수와 얼마나 차이가 나는지 알 수 없다는 단점이 있습니다. 즉, 추정의 정확도를 알 수 없다는 것입니다.
구간추정의 등장: 이러한 점추정의 한계를 보완하기 위해 등장한 것이 구간추정입니다. 구간추정은 모수가 특정 범위 안에 있을 가능성을 제시하여 추정의 불확실성을 고려합니다.
신뢰구간: 구간추정에서는 모수를 포함할 것으로 예상되는 범위를 신뢰구간이라고 합니다. 신뢰구간은 "95% 신뢰구간"과 같이 신뢰수준과 함께 제시됩니다. 신뢰수준은 모수가 신뢰구간 안에 포함될 확률을 의미합니다.
신뢰도: 신뢰수준을 신뢰도라고도 합니다. 95% 신뢰구간은 모수가 해당 구간 안에 포함될 확률이 95%라는 것을 의미합니다.
신뢰구간
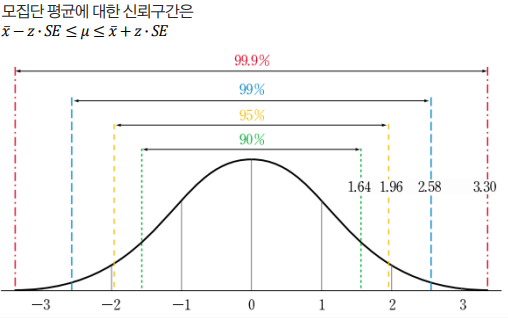
신뢰구간은 상한값과 하한값의 구간으로 표시됨
신뢰구간은 점추정량을 기준으로 상한과 하한을 설정하며, 그 구간 안에 모수가 포함될 확률을 신뢰수준으로 나타냄
신뢰수준이란 여러 번 표본을 추출했을 때, 계산된 신뢰구간 중 참된 모수를 포함할 확률을 의미함
모평균(𝜇)을 추정하고자 할 때, 표본평균을 𝑥̄ 표준오차를 𝑆𝐸라 함
표준오차란 ‘표본평균의 표준편차’로서, 여러 번의 표본추출로 계산된 표본평균들이 모평균으로부터 얼마나 떨어져 있는지를 나타내는 값
Test
가설
귀무가설
일반적으로 믿어온 사실 (기존 가설)
영가설, H0
기각이 목표
~ 없다, 같다
대립가설
귀무가설과 반대되는 가설로 연구의 목적이 됨 (주장하고자 하는 가설)
연구가설, H1
채택이 목표
~ 있다, 다르다
오류의 종류
1종 오류: 귀무가설이 참임에도 불구하고, 귀무가설을 기각하는 오류
실제로 효과가 없는데도 효과가 있다고 하는 것
2종 오류: 대립가설이 참임에도 불구하고, 대립가설을 기각하는 오류
실제로 효과가 있는데 효과가 없다고 하는 것
1종 오류가 더 위험!
예) 신약 개발을 했는데 신약이 효과가 없는데 있다고 하는것
유의 수준 (중요)
귀무가설이 참일 때, 이를 잘못 기각할 확률을 유의수준이라고 함
알파(a)로 표시함
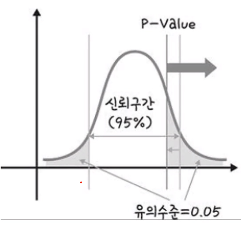
유의수준(a)을 0.05로 정했을 때, 도출된 유의확률(p-value)이 0.05보다 작으면 연구자나 조사자는 귀무가설을 기각할 수 있음
유의확률
p-Value 라고 하며, 귀무가설을 기각할 수 있는 최소한의 확률을 의미함
유의수준을 기준으로 유의확률이 유의수준보다 높으면 귀무가설을 채택하고,
유의수준보다 낮으면 귀무가설을 기각함
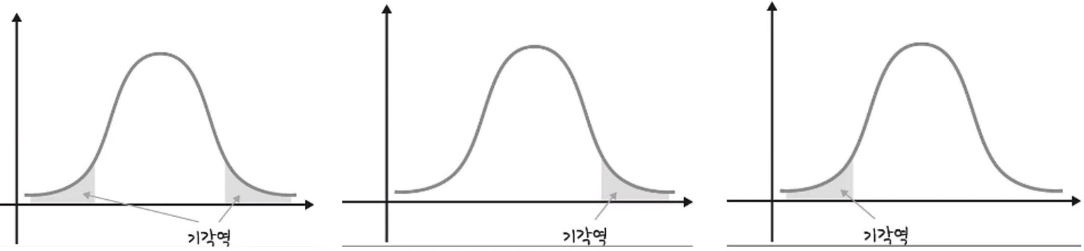
양측검정과 단측검정
양측검정이 단측검정보다 위험도가 낮은 것으로 알려져 있음
왜냐하면 단측검정은 한쪽 끝에 유의수준 전체를 배분하므로, 귀무가설을 잘못 기각할 확률이 더 높아짐
반면에 양측검정은 두 쪽에 나누어 기각역을 설정하므로, 같은 유의수준을 사용하더라도 귀무가설을 기각할 기회가 줄어듬
가설검정의 절차

t-test
t-검정
두 집단의 평균을 비교
표본의 평균을 사용하여 모집단의 평균에 대한 가설을 검증하는 방법
단일표본 t검정 예제)
250ml 음료는 정말 250ml가 들어있을까?
귀무가설: 음료의 용량은 250ml이다
대립가설: 음료의 용량은 250ml가 아니다
import pandas as pd
df = pd.read_csv('단일표본 t 검정 실습.csv', sep=',', encoding='CP949')
df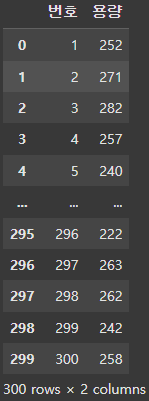
from scipy import stats
print(stats.ttest_1samp(df['용량'], 250))TtestResult(statistic=-4.673894108057419, pvalue=4.4766279943188894e-06, df=299)
ttest_1samp() 함수를 사용하여 단일표본 t-검정을 수행
250: 검정하려는 모집단 평균 값입니다. 즉, '용량'의 모평균이 250인지 검정합니다.
statistic: 계산된 t-통계량 값입니다.
pvalue: t-통계량에 해당하는 p-값입니다.
df: 자유도 (degrees of freedom)입니다.
결과 해석
- p-값 (4.4766279943188894e-06)이 유의수준 0.05보다 매우 작으므로, 귀무가설 (모평균 = 250)을 기각합니다.
- 따라서, '용량'의 모평균은 250이 아니라고 결론지을 수 있습니다.
- t-통계량이 음수 (-)인 것은 표본 평균이 검정하려는 모평균 값 (250)보다 작다는 것을 의미합니다.
'공부 > AI' 카테고리의 다른 글
| float 타입의 저장 방식, 부동소수점, IEEE 754 (0) | 2024.12.04 |
|---|---|
| 컴퓨터 공학 (CSE) - Computational Thinking (0) | 2024.12.04 |
| 통계학 Statistics 공부 for AI - 1 (0) | 2024.11.30 |
| 파이썬 컨테이너 Container 튜플 tuple (0) | 2024.11.28 |
| 파이썬 컨테이너 Container 딕셔너리 dict (0) | 2024.11.25 |